|
|
|
Vippor
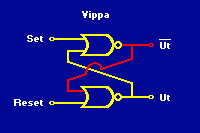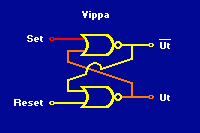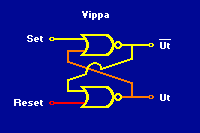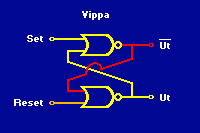
Två grindar kan tillsammans bilda en vippa som har två stabila tillstånd, eller "lägen". Blir det en spänning på den ena av ingångarna så ställer sig vippan i det ena läget. Vippan står sedan kvar i det läget även om man tar bort spänningen på ingången. Den står kvar ända tills det blir en spänning på den andra ingången, då slår den om till det andra läget och blir kvar där även om spänningen på ingången försvinner. På utgången kan man "känna av" i vilket läge vippan står, genom att känna av om där finns en spänning eller ej. Ofta finns av praktiska skäl även en alternativ utgång, som är den vanliga utgångens motsats.
| |
Vippa bestående av två NOR-grindar. Eftersom vippan står kvar i det läge den ställts i, kan den användas för att bygga upp minnen. Vissa (men inte alla) minnen i datorer består av vippor, t.ex. inne i datorns processor. Vippor kan även konstrueras på andra sätt än med två NOR-grindar. |
Om flera vippor kombineras kan de tillsammans lagra ett tal. Varje vippa kan bara "minnas" vilket av två lägen den står i, en bit. Om vi t.ex. har åtta vippor så kan de bilda 256 olika kombinationer av sina lägen. Man kan säga att åtta saker som var och en kan vara på två sätt, kan kombineras på 256 olika sätt (2 upphöjt till 8 är lika med 256). En liknelse är åtta enkronor, som var och en kan ligga med kronan eller klaven uppåt. Varje enkrona motsvarar en vippa, och hela gruppen av åtta bitar (eller bits) kallas en byte. En byte är åtta bitar tillsammans, och de 256 möjliga kombinationerna kan t.ex. betyda ett tal mellan 0 och 255.
Binära minnen
De två olika lägen som varje bit kan skifta mellan kan betyda 0 och 1. Eftersom det bara finns två lägen blir det bara två siffror, det fungerar som ett talsystem som bara har två siffror i stället för tio, det binära talsystemet. Tal i vårt vanliga decimala talsystem kan även lagras binärt, man kan tänka på det som att de kan översättas till det binära systemet. Det är så datorer lagrar saker, allt bryts ner till bitar som var och en är 0 eller 1, och flera bitar tillsammans bildar tal, bokstäver och annat, t.ex. färgpunkter i en bild. De allra snabbaste minnena i datorer (t.ex. inne i processorn) består av vippor, medan inte fullt så snabba minnen (t.ex. primärminnet, RAM) av kostnadsskäl och utrymmesskäl består av små kondensatorer och transistorer.
| Decimalt | Binärt |
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
| 8 | 1000 |
|
Allting i det binära talsystemet är likadant som i vanliga fall, den enda skillnaden är att det bara finns två olika siffror. Man räknar t.ex. likadant. Om man ska börja på noll och räkna uppåt tar man först de siffror som finns, i det här fallet bara 0 och 1. Sedan får man (precis som vanligt) ta till en sifferposition till, sätta en etta där, och sedan börja om i den första positionen. När man använt alla kombinationer som går att göra med två sifferpositioner tar man till ytterligare en tredje sifferposition, osv. Allt sker på samma sätt som i det decimala talsystemet vi är vana vid, enda skillnaden är att det finns färre olika siffror så det kommer snabbare att behövas fler sifferpositioner. Med tre positioner kan vi uttrycka åtta olika tal, t.ex talen 0 till 7. Med fyra positioner kommer vi upp i sexton olika tal, t.ex. talen 0 till 15 (15=1111). |
Adderare
Grindar kan också kombineras till kretsar som kan räkna med tal som lagrats binärt, till exempel ta ett tal plus ett annat. En sådan krets, adderare, finns i processorn i datorer. Till adderaren kommer talen genom ett antal ledningar, en ledning för varje sifferposition i det ena talet, och en ledning för varje sifferposition i det andra talet. Hur många ledningar som behövs (och hur många grindar som adderaren består av) beror på hur stora tal (hur många binära sifferpositioner) som ska kunna adderas.
Två tal som består av en enda bit var kan adderas med hjälp av en XOR-grind och en AND-grind. XOR-grinden tar in de två talen, och ger ut den högraste biten av summan. Om båda talen är 0 blir summan 0, om endera av talen är 1 (men inte det andra) blir summan 1. Om båda talen är 1 blir summan 10 (2 binärt) och XOR grinden ger 0 på utgången (den högraste siffran i summan 10). Den vänstraste siffran i summan fås av AND-grinden. Om båda talen är 1 så kommer AND-grinden att ge 1 på utgången, i alla andra fall ger dess utgång 0. En sådan krets kallas halvadderare.
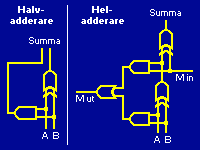
|
| En halvadderare kan addera två tal som består av en bit var. En heladderare tar hänsyn till en minnessiffra som kommer in från beräkningen av sifferpositionen till höger. Den beräknar en av sifferpositionerna i summan och lämnar ifrån sig en minnessiffra till beräkningen av sifferpositionen till vänster.
|
När tal som består av fler sifferpositioner än en skall adderas behöver kretsarna i adderaren ta med minnessiffran i beräkningen. Adderingskretsarna för varje sifferposition i summan (utom den allra högraste positionen) tar hänsyn till att det kan komma en minnessiffra från beräkningen av sifferpositionen till höger. Och om beräkningen av en viss sifferposition i summan ger en minnessiffra ut så skickas den vidare till beräkningen av sifferpositionen till vänster. En adderare som klarar det kallas heladderare och kan konstrueras av fem grindar.
Varje heladderare beräknar resultatet för "sin" sifferposition i summan. De kopplas ihop så att minnessiffran ut blir minnessiffran in till adderaren som beräknar sifferpositionen närmast till vänster. För den allra högraste sifferpositionen kan en halvadderare användas.
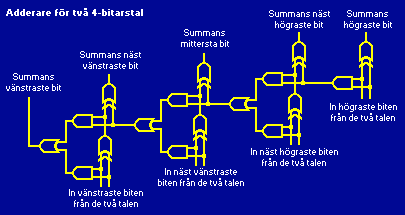
|
| Adderare för två positiva tal som består av fyra bitar var.
|
I datorer är adderare för tal som består av 32 eller ännu fler bitar vanliga. Med så många heladderare som kombinerats kan det bli en påtaglig väntetid innan minnessiffran successivt beräknats för alla sifferpositionerna till höger innan den kommer fram till heladderarna långt till vänster i kretsen. Mer avancerade kopplingar kan då användas som utför additionen snabbare. Ett annat fiffigt trick kan användas när tal skall subtraheras. Talet som skall subtraheras görs om till motsvarande negativa tal, och adderas sedan på vanligt sätt. Att addera det negativa talet är samma sak som att subtrahera det positiva. På så sätt kan adderare även användas till att subtrahera. Adderaren modifieras då en aning, i figuren ovan förutsätts att positiva heltal ska adderas.
|
|
|