|
|
|
Kondensatorer
Precis som motstånden gör kondensatorer en sorts motstånd mot ström. Men det finns en skillnad: kondensatorns bromsande verkan är olika beroende på strömmens frekvens. Har strömmen hög frekvens gör kondensatorn mindre motstånd, är frekvensen lägre gör kondensatorn mer motstånd. För ren likström är det tvärstopp, den släpper kondensatorn inte igenom alls.
Sådant frekvensberoende motstånd kallas reaktans, och det mäts i ohm precis som den vanliga resistansen. I formler betecknas reaktans med X, ibland tillsammans med ett C (om det är fråga om t.ex. kondensatorer) eller ett L (om det är fråga om t.ex spolar). Eftersom reaktans beror på strömmens frekvens kan man inte ange på en kondensator vad den har för reaktans, däremot kan man räkna ut vad reaktansen blir vid en viss frekvens. Den uträknade reaktansen gäller bara vid den aktuella frekvensen.
Kapacitans
I stället anges kondensatorns styrka (eller "storlek") som dess kapacitans. Kapacitans mäts i farad, vilket förkortas F. 1 farad är en väldigt hög kapacitans, mycket högre än hos de kondensatorer som normalt används i elektroniken. Därför anges ofta kapacitansen i mikrofarad (miljondels farad) som förkortas µF, eller nanofarad (miljarddels farad) som förkortas nF. För de minsta kondensatorerna används även picofarad (biljondels farad) vilket förkortas pF. I formler och liknande betecknas kapacitans med C.
|
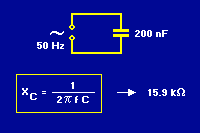
| En kondensators reaktans vid en viss frekvens kan räknas ut med formeln på bilden. Om en kondensator på 200 nF kopplas in i en krets med växelström på 50 Hz så kommer den att bromsa strömmen med drygt 15.9 kohm.
|
Exempel:
Kopplar man in en kondensator på 200 nF i en elektrisk krets där det flyter en växelström med frekvensen 50 hertz blir reaktansen vid den frekvensen drygt 15.9 kohm. Här är en steg-för-steg beskrivning hur man kan räkna:
1) Gör först om kapacitansen till farad. I formeln för reaktansberäkningen används kapacitansen i farad, och i kretschemat (och på kondensatorn) används i det här fallet nanofarad (nF). 1 nF är lika med en miljarddels farad, så 200 nF är lika med 0.0000002 farad.
2) Multiplicera ihop de 4 sakerna under delningsstrecket: 2 gånger pi gånger 50 gånger 0.0000002, vilket är lika med 0.000062831852. Har man en miniräknare med en knapp för pi så använder man den, annars kan man använda 3.1415926 som pi.
3) Tag 1 delat med det du nyss fick fram i steg 2: 1 delat med 0.000062831852 är lika med 15915.49458068, drygt 15.9 kohm.
Hade frekvensen varid den dubbla (100 Hz) hade kondensatorn bromsat strömmen hälften så mycket, och om kondensatorn varit dubbelt så stor (400 nF) hade också strömmen bromsats hälften så mycket. Hög frekvens på strömmen gör att den lättare tar sig igenom en kondensator, och hög kapacitans hos en kondensator gör att den lättare släpper igenom växelström.
Likström kan inte alls ta sig igenom en kondensator, men däremot inträffar något annat: kondensatorn laddas upp med energi. Den energin kan kondensatorn sedan avge om något ansluts till den, ungefär som om den vore ett litet batteri. Energiurladdningen blir dock mycket kortvarig om det är fråga om någorlunda normalstora strömmar. För en del digitala tillämpningar, t.ex. vissa typer av minnen, fungerar det dock utmärkt eftersom det här rör sig om väldigt svaga strömmar.
I grunden är en kondensator metallplattor på kort avstånd ifrån varandra. Trots att plattorna inte är i elektrisk kontakt med varandra påverkar de varandra tvärs över avståndet som skiljer dem åt. Det är denna påverkan som blir större ju högre frekvensen är. I praktiken kan kondensatorer konstrueras på olika sätt, som ligger mer eller mindre nära varianten med metallplattor. Kondensatorer med små kapacitanser är oftast av en konstruktion som innebär att det inte spelar någon roll vilket håll man vänder dem när de kopplas in. Detta gäller dock inte elektrolytkondensatorer som måste vändas åt rätt håll. Elektrolytkondensatorer är vanliga när det gäller lite högre kapacitanser, och har en märkning som talar om vilket anslutningsben som är vilket. Kondensatorer är dessutom vanligen märkta med den högsta spänning de kan anslutas till. Även kondensatorer med variabel kapacitans förekommer, till exempel trimkondensatorer som kan justeras genom vridning med en skruvmejsel. När mycket små kondensatorer används i minneskretsar och liknande enligt stycket ovan så konstrueras de med hög täthet direkt i integrerade kretsar.
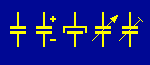
|
| Symboler för kondensatorer: allmän symbol, elektrolytkondensator (2 olika symboler), vridkondensator, trimkondensator.
(Symbolen finns även i en variant med den ena linjen böjd.)
|
Kondensatorkopplingar
Kopplas två eller flera kondensatorer parallellt blir den totala kapacitansen summan av de olika kapacitanserna. Kopplar man dem i serie blir den totala kapacitansen 1 genom summan av 1 genom de olika kapacitanserna. Detta är precis tvärt om som för motstånd: när kondensatorer parallellkopplas räknar man likadant som när motstånd seriekopplas, och när kondensatorer seriekopplas räknar man likadant som när motstånd parallellkopplas.
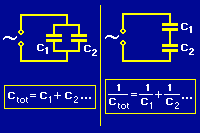
|
| Vid parallellkoppling av kondensatorer kan de olika kapacitanserna läggas ihop. Vid seriekoppling av kondensatorer blir beräkningen likadan som när motstånd parallellkopplas, och den totala kapacitansen blir alltid lägre än den minsta kondensatorns.
|
Exempel:
Om två kondensatorer på 400 och 800 pF parallellkopplas blir den totala kapacitansen 1200 pF, eller 1.2 nF om man hellre vill uttrycka det så. Om de i stället kopplas i serie blir den totala kapacitansen 1 genom 400 (vilket är lika med 0.0025) plus 1 genom 800 (vilket är lika med 0.00125), totalt 0.00375, och så slutligen 1 genom 0.00375 vilket är lika med 266.666667, alltså cirka 266.7 pF. (Om man som här använder värdena i picofarad som dom är (alltså utan att omvandla dem till farad först) så blir även svaret i picofarad. Är kapacitanserna angivna i olika enheter, eller om en massa andra saker är inblandade, som i reaktansformeln tidigare, kan man omvandla värdena till farad innan man sätter in dem i formeln.) När kondensatorer seriekopplas blir den totala kapacitansen alltid mindre än den minsta kapacitansen hos de inblandade kondensatorerna, annars har man räknat fel.
|
|
|