|
|
|
Motståndskopplingar
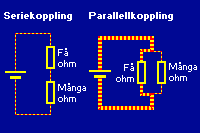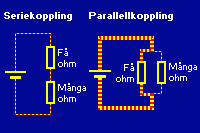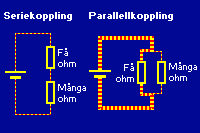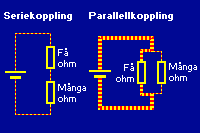
Är det bara fråga om ett enda motstånd (eller någon annan komponent som har en resistans) i en elektrisk krets är saken klar: all ström i kretsen passerar genom motståndet, och hela spänningen ligger över motståndet. Oftast finns det dock många saker i kretsen, och kopplingarna kan se ut på olika sätt. Antingen kan två eller flera komponenter, till exempel motstånd, kopplas "i en rad" efter varandra, eller så kan de kopplas "i bredd" bredvid varandra. I det första fallet, seriekoppling, finns det bara en väg för strömmen att gå, och det blir samma (lika stor) ström som flyter genom alla motstånden. I det andra fallet, parallellkoppling, finns två eller flera olika vägar för strömmen att gå, och strömmen kommer att dela upp sig mellan dem. Den uppdelningen (hur mycket ström som kommer att flyta genom varje motstånd) beror på motståndens resistans.
|
| Vid seriekoppling flyter samma ström genom motstånden. Vid parallellkoppling delar strömmen upp sig mellan de olika vägarna, och det kan flyta olika mycket ström genom motstånden.
|
Seriekoppling
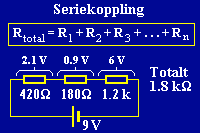
Den totala resistansen för motstånd som kopplats i serie är summan av deras resistanser. Om tre motstånd på 420 ohm, 180 ohm, och 1.2 kohm kopplats i serie är den totala resistansen 420 plus 180 plus 1200, vilket är lika med 1800 ohm, eller 1.8 k (kiloohm) om man vill uttrycka det så. Kopplar vi dem till en spänningskälla på 9 volt blir strömmen (enligt Ohms lag) 9 delat med 1800 vilket är lika med 0.005 ampere, eller 5 mA (milliampere). Samma 5 mA kommer alltså att flyta genom alla motstånden.
|
| Den totala resistansen hos ett antal seriekopplade motstånd är lika med summan av alla resistanserna. Strömmen genom dem är lika, och spänningen över dem beror på hur stor del av den totala resistansen de utgör. Om ett av motstånden (som här det på 180 ohm) utgör 10% av totalresistansen så kommer 10% av spänningen (0.9 volt) att ligga över det motståndet.
|
Spänningen över motstånden blir olika. Motståndet på 420 ohm utgör 23 och en tredjedels procent av det totala motståndet (420 delat med 1800 är lika med 0.2333333 när man slår det på en miniräknare). Då kommer även 23 och en tredjedels procent av spänningen att ligga över det motståndet. Spänningen blir 420 delat med 1800, gånger 9, vilket är 2.1 volt. (9:an kommer ifrån att den totala spänningen var 9 volt enligt stycket ovan.) Över 420-ohmsmotståndet kommer det alltså att ligga en spänning på 2.1 volt. Summan av de tre spänningarna över motstånden blir 9 volt, den totala spänningen från strömkällan.
Ett exempel på seriekoppling är den klassiska julgransbelysningen. Eftersom strömmen passerar genom alla lamporna på sin väg så slocknar alla lamporna om en enda går sönder eller skruvas ur. Spänningen över varje lampa blir liten eftersom de är så pass många. Det är på grund av seriekopplingen som många julgransbelysningar använder glödlampor på 14 volt trots att man kopplar in dem i vägguttaget. För alla glödlamporna tillsammans blir vägguttagets 230 volt lagom.
Parallellkoppling
Den totala resistansen för motstånd som kopplats parallellt är 1 delat med summan av 1 delat med varje resistans. Här är en steg-för-steg beskrivning av hur man kan göra:
1) Tag 1 delat med varje resistans så att du får ett antal nya tal.
2) Addera ihop dessa nya tal så att du får deras summa.
3) Tag 1 delat med denna summa så får du totalresistansen.
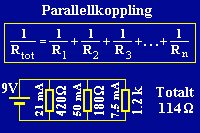
Om tre motstånd på 420 ohm, 180 ohm, och 1.2 kohm kopplats parallellt är den totala resistansen 1 delat med 420 (vilket är 0.002381), plus 1 delat med 180 (vilket är 0.0055556), plus 1 delat 1200 (vilket är 0.0008333), och tag sedan 1 delat med resultatet. Den totala resistansen blir drygt 114 ohm (0.002381 plus 0.0055556 plus 0.0008333 är lika med 0.0087699, och 1 delat med 0.0087699 är lika med 114.02639).
Kopplar vi kretsen till en spänningskälla på 9 volt kommer samma 9 volt ligga över alla motstånden. Den totala strömmen blir (enligt Ohms lag) 9 delat med 114.02639 vilket är lika med 0.0789291 ampere, eller cirka 78.9 mA (milliampere). Jämfört med när samma tre motstånd kopplades i serie blir nu alltså strömmen betydligt högre, eftersom totalresistansen är så mycket lägre i parallellkopplingsfallet. Vid parallellkoppling av motstånd blir den totala resistansen alltid lägre än det lägsta av motstånden, annars har man räknat fel.
|
| Den totala resistansen hos ett antal parallellkopplade motstånd kan beräknas med formeln på bilden. Spänningen över dem är lika, och strömmen genom dem beror på hur stor del av den totala resistansen de utgör, liten resistans medför högre ström. Strömmen genom de olika motstånden kan beräknas med Ohms lag.
|
Strömmen genom motstånden blir olika. Eftersom man vet spänningen (hela spänningen ligger över alla tre motstånden) och resistansen kan man använda Ohms lag för att räkna ut strömmen genom varje motstånd. Genom 420-ohmsmotståndet blir strömmen 9 delat med 420, vilket är lika med 0.0214286 ampere, eller drygt 21 mA (milliampere). Summan av strömmen genom de tre motstånden blir lika stor som den totala strömmen som tas ut från batteriet.
Ett exempel på parallellkoppling är när man kopplar in en massa saker till samma vägguttag. Alla sakerna får spänningen 230 volt, och ju fler saker man kopplar in desto större blir den totala strömmen som tas ut genom vägguttaget. Kopplar man in för mycket blir strömmen för hög, då går säkringen i proppskåpet.
|
|
|
Frågor och svar
Specialsektioner
