|
|
|
Resonanskretsar
Om nu spolar gör större motstånd ju högre strömmens frekvens är, och kondensatorer gör lägre motstånd ju högre strömmens frekvens är, vad händer då om vi kopplar ihop dem? Då får vi en resonanskrets, som kan utnyttjas för att antingen spärra för en viss frekvens, eller släppa igenom en viss frekvens. Vilket det blir beror på om vi seriekopplar eller parallellkopplar dem.
Parallellresonanskrets
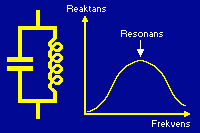
Vid parallellkoppling delar strömmen upp sig mellan de alternativa vägarna, och mest ström kommer att flyta där motståndet är lägst. Vid låga frekvenser är det lätt för strömmen att passera genom spolen, så då går det mesta den vägen, och vid höga frekvenser är det lätt för strömmen att passera genom kondensatorn, så då går det mesta den vägen. I båda fallen blir den totala bromsande effekten på strömmen liten. Mest bromsande blir parallellresonanskretsen för den frekvens där både spolen och kondensatorn ger lika mycket motstånd, där deras reaktans är lika stor. Denna frekvens är resonansfrekvensen för just den kondensatorn och spolen ihop. Om strömmen har just den frekvensen är ingen av vägarna lättare än den andra, och hälften av strömmen flyter genom kondensatorn och hälften genom spolen. Vid resonansfrekvensen är det totala motståndet mot strömmen störst. Ju mer frekvensen avlägsnar sig (uppåt eller nedåt) från resonsansfrekvensen, desto lättare blir det för strömmen att passera.
|
| En parallellresonanskrets gör störst motstånd vid resonansfrekvensen, där spolens och kondensatorns reaktanser är lika stora. Den kan användas för att filtrera bort en oönskad frekvens och släppa igenom andra frekvenser lättare. (Principkurva.)
|
Serieresonanskrets
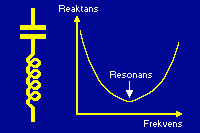
Om man i stället kopplar kondensatorn och spolen i serie, måste strömmen alltid ta sig igenom båda komponenterna. Det räcker då med att någon av dem gör mycket motstånd för att det ska bli ett stort totalt motstånd. Vid låga frekvenser gör kondensatorn mycket motstånd, och vid höga frekvenser gör spolen mycket motstånd. Minst totalt motstånd blir det när spolens och kondensatorns motstånd är lika stora. Detta kallas även hos serieresonanskretsar för resonansfrekvensen, och är fortfarande när spolens och kondensatorns reaktanser är lika stora. Skillnaden är att hos serieresonanskretsar är motståndet minst vid resonansfrekvensen. Ju mer strömmens frekvens avlägsnar sig (uppåt eller nedåt) från resonsansfrekvensen, desto svårare blir det för strömmen att passera.
|
| En serieresonanskrets gör minst motstånd vid resonansfrekvensen, där spolens och kondensatorns reaktanser är lika stora. Den kan användas för att släppa igenom en önskad frekvens och filtrera bort andra frekvenser, till exempel i en radio eller TV. (Principkurva.)
|
Resonansfrekvens
Det som bestämmer vad resonansfrekvensen blir är kondensatorns kapacitans, och spolens induktans. Det är de enda två värden som behövs för att räkna ut resonansfrekvensen. Vilken spole och kondensator man än tar, så finns det en viss resonansfrekvens när man kopplar ihop dem. En större kondensator ger en lägre resonansfrekvens. Samma sak gäller för spolen: ju större spole desto lägre resonansfrekvens. Om vi både tar en större spole och en större kondensator blir resonansfrekvensen kraftigt lägre. Vill man att resonansfrekvensen skall vara hög använder man små kondensatorer och spolar.
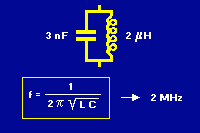
|
| Resonansfrekvensen kan räknas ut med formeln på bilden. Det spelar ingen roll om det är en serie- eller parallellresonanskrets, samma formel används för att få fram resonansfrekvensen.
|
Här är en steg-för-steg beskrivning av hur man kan räkna:
1) Tag kapacitansen (i farad) gånger induktansen (i henry) så att du får ett nytt tal: 0.000000003 gånger 0.000002 är lika med 0.000000000000006.
2) Tag kvadratroten ur det nya talet (det du fick fram i steg 1) så att du får ytterligare ett nytt tal: kvadratroten ur 0.000000000000006 är lika med 0.00000007746.
3) Tag det senaste talet (det du fick fram i steg 2) gånger 2 gånger pi, så att du får ännu ett nytt tal: 0.00000007746 gånger 2 gånger 3.1415926 är lika med 0.00000048669.
4) Tag 1 delat med talet du fick fram i steg 3, så får du fram resonansfrekvensen: 1 delat med 0.00000048669 är lika med 2054700, drygt 2 MHz.
Om man har en spole och en kondensator i en resonanskrets, och sedan byter till en dubbelt så stor kondensator samtidigt som vi byter till en hälften så stor spole, så ändras inte resonansfrekvensen. Det samma gäller om man halverar kondensatorns kapacitans och samtidigt dubblerar spolens induktans, resonansfrekvensen ändras inte. Sådana ändringar tar ut varandra. Stor påverkan på resonansfrekvensen blir det om vi ökar både spolen och kondensatorn (resonansfrekvensen sjunker) eller om vi minskar både spolen och kondensatorn (resonansfrekvensen stiger).
|
|
|